اهمية المصفوفات في حياتنا
- تشكل المصفوفات جزءاً أساسياً في دراسة العديد من الظواهر العلمية، وهي حاضرة بقوة في الرسوم البيانية، خاصة تلك التي تظهر معلومات في ثلاثة أبعاد.
- تلعب المصفوفات دوراً هاماً في تطوير التطبيقات في مجالات مثل الفيزياء والهندسة والبصريات، مما يجعلها أداة متعددة الاستخدامات وفعّالة.
- بالإضافة إلى ذلك، تُعتبر المصفوفات عنصراً مهماً في النظريات الاحتمالية وعلم الإحصاء، كما تُستخدم لوصف العديد من الأنظمة الاقتصادية بدقة.
- يستفيد مجال علوم الكمبيوتر من الرسوميات في تطوير الخوارزميات وتنظيم المعلومات على الصفحات.
- يشمل الفهم العميق للتحليل الكلاسيكي على إدراك أهمية مواضيع مثل الدوال الأسية وفهم المشتقات في أبعاد متعددة.
- تلعب التحويلات الخطية دوراً رئيسياً في معالجة وعرض الصور ضمن التطبيقات المختلفة.
- هذه الأدوات تجد استخداماتها في العديد من المجالات الأخرى التي تبرز أهميتها في البحث والتطوير.

تعريف المصفوفة
المصفوفة هي ترتيب لأعداد تُصف في أشكال صفوف وأعمدة، وهذه الأعداد يمكن أن تكون عبارة عن قيم حقيقية أو عقدية.
هذا الترتيب يعمل كدالة رياضية خطية تقوم بتحويل معلومات من مجموعة بداية إلى أخرى نهائية ثابتة، يمكن لهذه المجموعات أن تحتوي على أعداد صحيحة، عقدية، دوال رياضية، أو حتى مجموعات من دوال. في الكتابة، نستخدم أقواس مربعة أو هلالية لتنظيم هذه الأرقام ضمن المصفوفة.
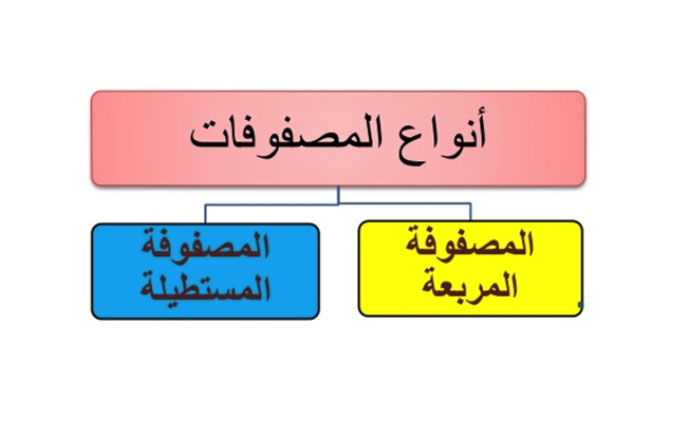
أنواع المصفوفات
1- المصفوفة المستطيلة: تُعرَّف المصفوفة غير المربعة بأنها تلك التي تختلف فيها أعداد الصفوف عن أعداد الأعمدة. بمعنى آخر، عدد الصفوف فيها إما أن يكون أكبر من عدد الأعمدة أو أقل منه.
2- المصفوفة الصفرية(null or matrix): عندما تحتوي المصفوفة، التي قد تكون ذات شكل مستطيلي أو مربعي، على عناصر تساوي جميعها الصفر، فإنها تُعرف بالمصفوفة الصفرية.
3-المصفوفة القطرية (Diagonal matrix): تتألف المصفوفة المربعة من عناصر تُحدُّد قيمة الصفر في جميع الخانات باستثناء تلك التي تقع على القطر الرئيس، الذي يمتد من الزاوية اليمنى العليا إلى الزاوية اليسرى السفلى، حيث تختلف هذه العناصر في قيمها العددية ولا تكون صفراً.
4-مصفوفة الوحدة (unit matrix): تتكون هذه المصفوفة من أشكال مربعة حيث تحتوي كل خاناتها على قيمة صفر باستثناء الخانات الممتدة على القطر الأساسي التي تتخذ قيمة واحد. تلك الخصائص تميزها عن المصفوفة القطرية.
5-مصفوفة المتجهات (vectors matrix): متجه الصف ينطوي على مصفوفة أفقية تحتوي على أعمدة عديدة وصف واحد فقط. بينما يُعرف متجه العمود بأنه مصفوفة رأسية تشتمل على صف واحد فقط ولكن العديد من الأعمدة.
6-المصفوفة المبدلة (Transpose matrix): عندما نأخذ مصفوفة بأبعاد (م × ق)، حيث (م) هو عدد الصفوف و(ق) هو عدد الأعمدة، ونقوم بتبديل مكان الصفوف مع الأعمدة محافظين على ترتيب العناصر أو عكسه، نحصل على مصفوفة جديدة تُسمى المصفوفة المبدلة، والتي تُرمز لها ب(أ’ (م × ق)).
7-المصفوفة المتماثلة (Symmetric matrix): في حالة وجود مصفوفة مربعية بأبعاد (م × ق)، وتغيير صفوف هذه المصفوفة بأعمدتها وفقًا للترتيب الأصلي، فإنها تتحول إلى ما يعرف بالمصفوفة المبدلة.
عندما تظل العناصر المقابلة بين المصفوفة الأصلية والمصفوفة المبدلة دون تغيير، تعرف هذه المصفوفة بأنها متماثلة. خاصية أخرى للمصفوفة المتماثلة هي أن العناصر الموجودة على جانبي القطر الرئيسي تكون مطابقة بعضها لبعض.
8-المصفوفة القياسية (Scarler Matrix): تتكون المصفوفة من مجموعة عناصر تتحدد قيمتها بضرب كل العناصر الموجودة على القطر الرئيسي في قيمة ثابتة معينة. هذا يؤدي إلى تشكيل مصفوفة أساسية حيث تكون جميع العناصر الموجودة على القطر متطابقة.
9- المصفوفة الشاذة أو المنفردة (Singular matrix): عندما تكون مصفوفة ما ذات شكل مربع ومحدد قيمها يساوي صفر، تُعرف هذه المصفوفة بأنها مفردة، بينما في حال كان المحدد مختلفاً عن صفر، تُسمى المصفوفة بالمصفوفة العادية أو المنتظمة.
10-المصفوفة المربعة(square matrix): تُعرف هذه النوعية من المصفوفات بأن أعداد الصفوف فيها تتطابق مع أعداد الأعمدة.

ما هو حجم المصفوفات؟
في الرياضيات، تتألف المصفوفة من صفوف وأعمدة، ويُعبّر عن أبعادها باستخدام وصف يشير إلى عدد الصفوف والأعمدة.
يُشار إلى هذه الأبعاد بالصيغة (م، ن)، حيث “م” تمثل عدد الصفوف و”ن” عدد الأعمدة. الرموز الأخرى مثل (وم × ن) أو (م ن-by) تُستخدم أيضًا للدلالة على تركيب المصفوفة من حيث الصفوف والأعمدة.
في عالم الرياضيات، يعرف مصطلح نواقل التوالي بأنه يصف المصفوفات ذات الصف الواحد فقط، بينما المصفوفات التي تتكون من عمود واحد تُعرف بناقلات العود.
المصفوفة التي تكون بها الأعمدة والصفوف مُتساوية وتعدّ واحد تُسمى المصفوفة المربعة، إذا كانت المصفوفة خالية تماماً من الصفوف والأعمدة فهي تُعرف بالمصفوفة الفارغة، في حين تُسمى المصفوفات التي ليس لها حدود محددة في عدد الأعمدة والصفوف بالمصفوفات اللانهائية.